Get To Know PowerFX - Exp()

🧠 Introduction

Exponential growth isn’t just a buzzword - it’s real. And PowerFX gives you the tools to use it. The Exp() function brings advanced, scientific calculation into your Power Apps, whether you’re building for business, finance, or research.

The Exp() function raises the mathematical constant e (approximately 2.718) to the power you give it.

What is constant e? Euler's number, denoted by 'e', is an irrational and transcendental mathematical constant approximately equal to 2.71828. 

🧐 Why it's important in Math, Physics and even Finance:

I've tried to write quick and easy explanation and it turn's out, to get to the point it's not that easy - Not that I've tried.

Rather jump back in time and dig for math notes from collage, I've decided to engage AI friend for some help and write a description why is it important and where it's used. Which AI You might ask - Copilot, ChatGPT, Perplexity or other Gemini - let's keep that classified for marketing purposes 😂 nevertheless answers are quite similar - seems like resources also 👀

Euler's Number can be defined in a few ways:

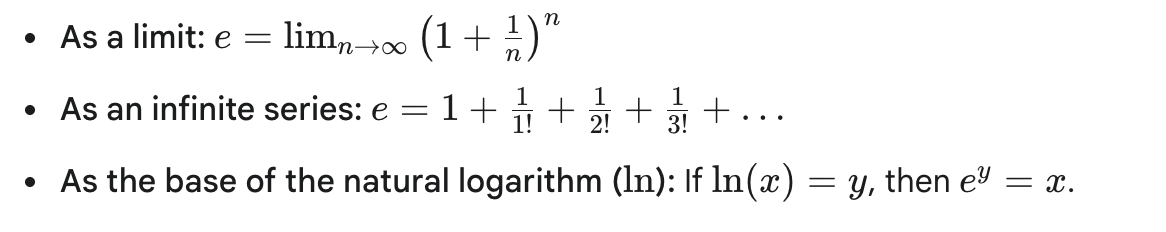
Euler's Number 'e' is fundamental because it describes processes where the rate of change of a quantity is proportional to the quantity itself. This "natural" rate of change makes it ubiquitous in modeling real-world phenomena.

• Calculus: The exponential function f(x)=e^x unique because its derivative (rate of change) is equal to itself:

  d/dx e^x = e^x. This property vastly simplifies calculations involving continuous change. It's also the inverse of the natural logarithm

• Differential Equations: Many natural processes are described by differential equations where the rate of change depends on the current state. Solutions to these often involve ex.
• Growth and Decay:
  • Population Growth: Models of populations growing without limits often use e^x.
  • Radioactive Decay: The exponential decay of radioactive isotopes is described using 'e'.
  • Cooling/Heating: Newton's Law of Cooling/Heating involves 'e' to model how temperature changes over time.
    

• Waves and Oscillations: Euler's identity (e^iπ+1=0) beautifully connects five fundamental mathematical constants (e, i, π, 1, and 0) and is crucial in understanding complex numbers, which are used to describe alternating currents, quantum mechanics, and wave phenomena.
• Probability and Statistics:
  • Normal Distribution (Bell Curve): The formula for the standard normal distribution involves e^−x2/2
  • Poisson Distribution: This distribution, which models the number of events occurring in a fixed interval of time or space, also uses 'e'.

Euler's Number in the Financial World - have You ever heard of continuous compounding? 

• Continuous Compound Interest: The formula for continuously compounded interest is A=Pe^rt, where:
  • A = the future value of the investment/loan, including interest
  • P = the principal investment amount (the initial deposit or loan amount)
  • r = the annual interest rate (as a decimal)
  • t = the time the money is invested or borrowed for, in years This formula calculates the theoretical maximum amount of interest that can be earned on an investment, assuming interest is compounded infinitely often.
• Financial Modeling: 'e' appears in various complex financial models, such as:
  • Black-Scholes Model: A fundamental model for pricing options, which assumes asset prices follow a log-normal distribution, involving continuous-time processes.
  • Risk Management: Used in models for continuously changing financial variables.

🧐 Euler's Number Quick Summary

Euler's Number value is used in:

• Growth modeling
• Interest rate compounding
• Scientific formulas
• Data visualisation

And as the base of Natural Algorithm.

🧐 What Exp() function does in PowerFX?

So much introduction of Euler's Number to finally get to the chase 😂 

Exp() calculates Euler's Number e (approximately 2.718) to power of provided exponent. So, Your input is just the exponent, and output of Exp() is e^{Provided Exponent}

Perfect for scientific and financial models! 🤯

🧪 Function Syntax

💡 Example

Canvas Apps are mostly - but not always - used for business automations, therefore I do not see valid example to share at the moment. 

Being totally transparent with You - I never had a business justification or a valid need to use Exp() in other scenario than to educate myself, or do some testing for You.

Maybe that day will come, who knows! Currently we have the power of knowledge - being sure this function is here with us. Whenever the need will come - We will be ready 🤩

To be sure I've asked our AI friends to give a hand with my assumption.

💼 Common Use Cases

✅ Score Normalisation:
👀 Give exponentially higher points as a user levels up - common in trainings, gamification, certification progress learning. 

✅ Time-Based Data Decay (e.g. Relevance Score)
👀 Older records can lose “relevance” in dashboards or prioritization views - discussable

✅ Animation Speed or Delay Curve

✅ Impact Modeling in visualisations

✅ Threat Level or Risk Index Growth

✅ Productivity vs Time Chart

⚠️ Common Pitfalls

❌ Expecting Exp() to work as Power() - blindly mistake

👀 Exp() takes Euler's Number as base - always. You cannot change the base as the only input You can provide - is the power of exponent

❌ Misunderstanding its simplicity
👀  Exp() only provides Euler's Number raised to provided exponents. That is all. Don't overthink it.

❌ Misunderstanding the Error Handling
👀  There is no Error Handling included in Exp() 

❌ Won’t work on text:
👀 Valid input are numbers only. If number is provided as text - wrap in Value() first

❌ Providing big exponential input:
👀 Feeding large inputs into Exp() leads to very large outputs, be sure for what You need it to. 

❌ Expecting Negative Inputs to Return Negatives
👀 Exp(-x) never returns negative values. It returns a positive decimal in range 0 and 1. The bigger negative input, the closer to 0 we go, nevertheless remember that Canvas Apps are not working by default in more than 8 decimal places.   
👀 Exp(-18) will provide output 0.00000002, but Exp(-19) can show 0.

❌ Ignoring Decimal Precision
👀 Exp() results often have long decimals. You need it for something, therefore analyse if Round() the number is required for Your scenario. Topic for another blog post 

❌ Chaining Exp() Too Aggressively
👀 Stacking multiple Exp() calls can cause massive numeric overflow.

❌ Forgetting It’s Not Reversible by Power()
👀 Only Ln() can reverse Exp(), not Power() - Topic for another blog post 😎

🧾 Summary

PowerFX stores the power to create exponential growth with one simple function - Exp()

👉 Exp() raises Euler's Number e (~2.718) to a given power — excellent for growth, decay, and simulations.

👉 Exp() is great to know and is academically useful, but almost never essential in real-life Canvas Apps, unless Your application is simulating a mathematical pattern or have custom and unusual analytical approach.

👉 It’s the inverse of Ln().

👉 Exp() is good-to-know but rarely-needed function - I'll risk that statement. If I am wrong - let me know!

👉 Example usage for level upsystems, time-based logic, and data transformation in advanced Power Apps.

👉 Combine with Ln(), Power(), or Round() to create custom formulas with real-world intelligence.

💡 Want More?

We are just getting started to Unleash The Power of Productivity with Canvas Apps & PowerFX

👉 Watch the Reels 🎥 : TikTok | Instagram | YouTube Shorts
👉 Swipe the Carousel: LinkedIn | Instagram

FYI: URLs will be activated soon 😃

Follow as we break down PowerFX -  function by function -  in the most visual, practical way on the internet.